Reinforced Concrete Analysis

reinforced concrete beam

Reinforced concrete analysis is performed at a given section for either axial force and bending moment or transverse shear loads. The axial force and bending moment analysis usually idealizes the stress-strain behavior of the concrete with a rectangular stress block to simplify the calculations. More detailed, moment curvature analysis may be performed with more complex stress-strain relationships.

Reinforced Concrete Analysis Types:

  1. Axial Force and Bending Moment
    1. Pure flexure design example
  2. Moment Curvature Analysis

Axial Force and Bending Moment:

Reinforced concrete analysis for axial force and bending moment is usually performed by assuming a given strain value at the extreme compression fiber with a linear strain distribution over the depth of the section.  The stress distribution typically assumes a rectangular stress block with a depth equal to some fraction of the neutral axis depth and a magnitude equal to some fraction of the concrete compressive strength.

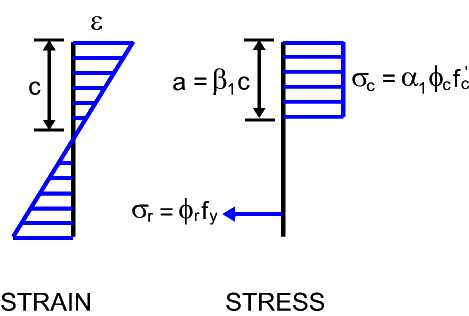
Stress-strain diagram

Design Parameters:

  1. Stress and strain

  1. Stress block

  1. Reduction factors (American, ACI 318)

Note: Strength reduction factors are used in the American codes, both ultimate strength design and load-resistance factor design. These factors are applied to the computed strength based on the mode of failure.

  1. Resistance factors (Canadian, CSA A23.3)

Note: Resistance factors are used in the Canadian codes and are applied directly to the material strengths without regard to the mode of failure.

Pure Flexure Design Example:

Determine the bending moment resistance of a rectangular beam with tension reinforcement and no axial loads.

Beam section

Depth to reinforcing = d = 21 inches
Beam width = b = 12 inches
Reinforcing steel area = As = 3.0 in2
Concrete compressive strength = f'c = 4000 psi
Reinforcing yield strength = fy = 60000 psi

  1. Determine moment capacity per ACI 318

Maximum concrete strain = e = 0.003
Reduction factor for flexure = f = 0.90
 Ratio of average concrete stress = a1 = 0.85
Ratio of stress block depth = b1= 0.85

  1. Solve for a using the SF = 0.

As fy = a b a1 f'c
3.0(60000) = a (12)(0.85)(4000)
a = 4.41 inches

  1. Determine moment from force couple

f Mn = f Asfy (d - a / 2)
f Mn = 0.9(3.0)(60)(21 - 4.41 / 2) / 12
f Mn = 254 k-ft

  1. Determine moment capacity per CSA A23.3

Maximum concrete strain = e = 0.0035
Concrete resistance factor = fc = 0.60
 Reinforcement resistance factor = fr = 0.85
 Ratio of average concrete stress = a1 = 0.81
Ratio of stress block depth = b1= 0.9

  1. Solve for "a" using the SF = 0.

fr As fy = a b a1 fc f'c
0.85(3.0)(60000) = a (12)(0.81)(0.6)(4000)
a = 6.56 inches

  1. Determine moment from force couple

Mr = fr Asfy (d - a / 2)
Mr = 0.85(3.0)(60)(21 - 6.56 / 2) / 12
Mr = 226 k-ft